超级旋转系统

这篇文章需要改进。你可以帮助俄罗斯方块中文维基编辑。

超级旋转系统（Super Rotation System，简称 SRS），别称「标准旋转系统」（Standard Rotation System），是一套由俄罗斯方块准则定义，供四连方块使用的旋转系统。该系统决定了方块生成、旋转、踢墙的方式。大多数现代官方俄罗斯方块都采用了该旋转系统，而现代非官方方块的旋转系统大都以 SRS 为基础。

SRS 最早可追溯至1991年的 Tetris 2 + BomBliss，这一版本中引入了 SZI 三种方块的另外两种朝向。在1993年的俄罗斯方块武斗外传中， BPS 修改了 TLJ 三块的初始朝向，让它们生成时最长边朝下。踢墙系统直到 2001 年的 Tetris Worlds 才首次出现。至此，SRS 基本成型。亨克·罗杰斯为了让所有新发布的俄罗斯方块游戏符合准则，要求 Arika 在 2005 年发布的俄罗斯方块特级大师3：恐怖本能中附带 SRS。在 TGM3 和 TGM4 中，准则的规则被称作「World」规则，以致敬 Tetris Worlds。

初始朝向和位置

七种四连方块的四个朝向。最左侧为初始状态，右侧三列分别为顺时针旋转一至三次后的状态。圆圈代表旋转中心。

初始朝向如右图所示。

• 所有方块在场地上方水平生成
• I 块与 O 块在中部生成，其他三格宽的四连方块偏左一格生成。
• J 块、L 块与 T 块背部朝下生成
• Tetris Worlds 中，方块在第 22 与 23 行生成（I 块于 22 行生成）
  • 之后的大多数游戏中，方块生成的位置下降了一格
  • 部分游戏如俄罗斯方块 99 采取初始生成位置较低，若窒息再抬高到最高第 21、22 行的生成方法
  • 俄罗斯方块效应的方块生成位置又下降一格，于第 20 与 21 行生成

基本旋转

基本旋转方式如右图所示。 注意：

• 若没有阻挡，方块只会绕着一个固定点旋转，称作「旋转中心」，在图中用圆圈标出。
• 基本旋转与纯粹的几何旋转完全相同，与其他部分旋转系统（如世嘉旋转系统与雅达利旋转系统）不同，旋转不会导致额外的位移。
• S、Z、I 三块有四种朝向。
• I、O 的旋转中心位于格点；Z、S、J、L、T 的旋转中心位于方格中心。

踢墙

方块尝试旋转时，若旋转的终点被原有的方块或场地边上的墙阻挡，系统会对方块测试一系列位移值（即踢墙），以进入其他位置。 注意：

• 旋转尝试通常测试五个位置（包括基本旋转）；若都不可用，则旋转失败。
• 测试的位置由初始朝向和最终朝向决定。由于可顺时针和逆时针旋转方块，共有四种初始朝向和两个最终朝向。因此，每种方块共有八种可能的状态，须给定八组踢墙表。
• 位置通常用 (x , y) 踢墙值描述，踢墙值给出了方块踢墙时的位移量；通常以向右为 x 的正方向，向上为 y 的正方向。如(-1,+2) 表示向左一格、向上两格。
• Z、S、J、L、T 块踢墙表相同，I 块有独自的踢墙表，O 块没有踢墙。
• 通常用数字和字母描述旋转方向。本条目中，描述方式如下：
  • 0 = 初始态
  • R = 初始态顺时针旋转（右转）后的状态
  • 2 = 初始态旋转 180° 后的状态
  • L = 初始态逆时针旋转（左转）后的状态

Z、S、J、L、T 方块踢墙表

	测试 1	测试 2	测试 3	测试 4	测试 5
0->R	( 0, 0)	(-1, 0)	(-1,+1)	( 0,-2)	(-1,-2)
R->0	( 0, 0)	(+1, 0)	(+1,-1)	( 0,+2)	(+1,+2)
R->2	( 0, 0)	(+1, 0)	(+1,-1)	( 0,+2)	(+1,+2)
2->R	( 0, 0)	(-1, 0)	(-1,+1)	( 0,-2)	(-1,-2)
2->L	( 0, 0)	(+1, 0)	(+1,+1)	( 0,-2)	(+1,-2)
L->2	( 0, 0)	(-1, 0)	(-1,-1)	( 0,+2)	(-1,+2)
L->0	( 0, 0)	(-1, 0)	(-1,-1)	( 0,+2)	(-1,+2)
0->L	( 0, 0)	(+1, 0)	(+1,+1)	( 0,-2)	(+1,-2)

I 方块踢墙表

	测试 1	测试 2	测试 3	测试 4	测试 5
0->R	( 0, 0)	(-2, 0)	(+1, 0)	(-2,-1)	(+1,+2)
R->0	( 0, 0)	(+2, 0)	(-1, 0)	(+2,+1)	(-1,-2)
R->2	( 0, 0)	(-1, 0)	(+2, 0)	(-1,+2)	(+2,-1)
2->R	( 0, 0)	(+1, 0)	(-2, 0)	(+1,-2)	(-2,+1)
2->L	( 0, 0)	(+2, 0)	(-1, 0)	(+2,+1)	(-1,-2)
L->2	( 0, 0)	(-2, 0)	(+1, 0)	(-2,-1)	(+1,+2)
L->0	( 0, 0)	(+1, 0)	(-2, 0)	(+1,-2)	(-2,+1)
0->L	( 0, 0)	(-1, 0)	(+2, 0)	(-1,+2)	(+2,-1)

踢墙实例：
需要方块从初始位置左转，查上表可得，踢墙测试为 ( 0, 0), (+1, 0), (+1,+1), ( 0,-2), (+1,-2)。

1. 初始位置 尝试从初始位置 逆时针旋转（0->L）	2. 测试 1，( 0, 0) 失败（基础旋转失败）	3. 测试 2，(+1, 0) 失败。
4. 测试 3，(+1,+1) 失败。	5. 测试 4，( 0,-2) 失败。	6. 最终位置 测试 5，(+1,-2) 成功。

踢墙详细图解

详见 SRS 踢墙图解。

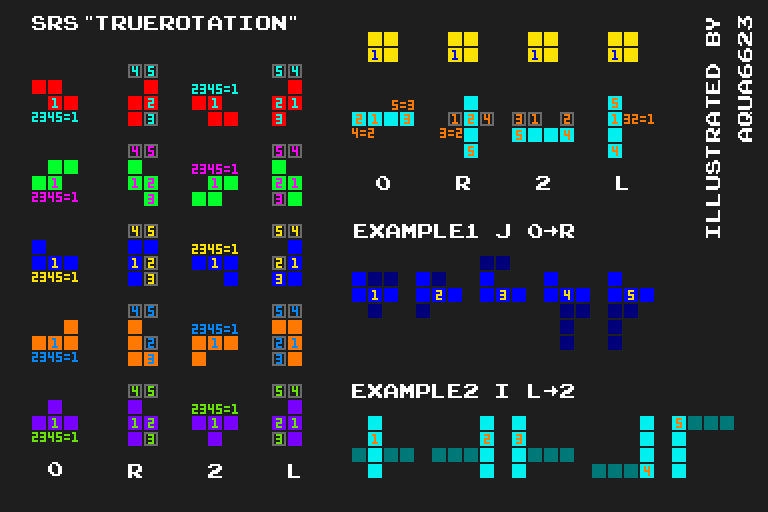
准则中描述的工作原理

准则描述的 SRS「真正的旋转」

在泄露的 2009 年准则中，俄罗斯方块公司实际上并没有直接采用将 (x, y) 位移量赋予八种不同的旋转，而是为四种朝向设置了数个锚点（Rotation Points），每个锚点拥有一个编号；试图应用第 n 位移时，将两个编号为 n 的锚点对齐，于是两方块的相对位置就是第 n 位移（见右图）。该方法被 HardDrop 论坛用户 nightmareci 称为「真正的旋转」（True Rotation）。
可以推得，这种方法同时满足两个性质：

• 若每次旋转都应用第 n 位移，则向同一个方向旋转四次后，方块必定回到原位；
• A 转向 B 时的所有位移与 B 转向 A 时的位移一一对应，方向相反，即大多数踢墙可逆。

因此，SRS 实际上隐式定义了 180° 旋转位移表，表内的值相当于一个块进行两次顺时针/逆时针旋转，同序号的位移矢量叠加。

但通过这种方式定义的 180° 旋转：

• Z、S、J、L、T 五块的水平方向和没有踢墙没有差别，竖直方向只多出了横向位移两格；
• O 块旋转后没有区别；
• I 块由于锚点不对称，有一些相当诡异的踢墙。

综合来看实用意义不大。

Z、S、J、L、T 方块锚点（值为相对于旋转中心的位置，下同）

姿态	锚点 1	锚点 2	锚点 3	锚点 4	锚点 5
0	( 0, 0)	( 0, 0)	( 0, 0)	( 0, 0)	( 0, 0)
R	( 0, 0)	(+1, 0)	(+1,-1)	( 0,+2)	(+1,+2)
2	( 0, 0)	( 0, 0)	( 0, 0)	( 0, 0)	( 0, 0)
L	( 0, 0)	(-1, 0)	(-1,-1)	( 0,+2)	(-1,+2)

I 方块锚点

姿态	锚点 1	锚点 2	锚点 3	锚点 4	锚点 5
0	( 0, 0)	(-1, 0)	(+2, 0)	(-1, 0)	(+2, 0)
R	(-1, 0)	( 0, 0)	( 0, 0)	( 0,+1)	( 0,-2)
2	(-1,+1)	(+1,+1)	(-2,+1)	(+1, 0)	(-2, 0)
L	( 0,+1)	( 0,+1)	( 0,+1)	( 0,-1)	( 0,+2)

O 方块锚点

姿态	锚点 1	锚点 2	锚点 3	锚点 4	锚点 5
0	( 0, 0)	仅有一个锚点
R	( 0,-1)
2	(-1,-1)
L	(-1, 0)

通过锚点计算位移量的实例：

J 块状态 0 的锚点为：( 0, 0), ( 0, 0), ( 0, 0), ( 0, 0), ( 0, 0)
J 块状态 R 的锚点为：( 0, 0), (+1, 0), (+1,-1), ( 0,+2), (+1,+2)

( 0, 0) - ( 0, 0) = ( 0, 0)
( 0, 0) - (+1, 0) = (-1, 0)
( 0, 0) - (+1,-1) = (-1,+1)
( 0, 0) - ( 0,+2) = ( 0,-2)
( 0, 0) - (+1,+2) = (-1,-2)

因此，基于“真正的旋转”，J 方块 0->R 的踢墙位移为（与其基本旋转相同）：( 0, 0), (-1, 0), (-1,+1), ( 0,-2), (-1,-2)。

但准则所描述的方法并没有显式规定旋转中心，如果将 1 号锚点视作旋转中心，则旋转中心总是在方格中心，而非网格点上。O、I 两块的旋转中心不是其几何中心，其旋转时会颠簸，准则中设置的锚点抵消了颠簸，使得其看上去像绕着一个格点旋转。

但固定旋转中心+踢墙表的描述方法比锚点对齐的方法更简单、直观、通用，因此更被社区广泛接受。

farter 认为这只是一种分析角度。「可逆、成环」性质确实存在，但不确定官方是否如此实现，旋转中心不一定必须定义在格心。

Arika SRS

Arika 的俄罗斯方块特级大师系列诞生于准则之前，但在准则出现之后俄罗斯方块公司要求 Arika 将 SRS 作为默认旋转系统。因此 Arika 在系列的 TGM3 与 TGM Ace 中引入了自己版本的 SRS，与准则略有不同。

在 Arika SRS 中，JLSTZ 方块的踢墙与准则相同；然而，I 块的踢墙表不同，如下所示：

Arika I 块踢墙表

	测试 1	测试 2	测试 3	测试 4	测试 5
0->R	( 0, 0)	(-2, 0)	(+1, 0)	(+1,+2)	(-2,-1)
R->0	( 0, 0)	(+2, 0)	(-1, 0)	(+2,+1)	(-1,-2)
R->2	( 0, 0)	(-1, 0)	(+2, 0)	(-1,+2)	(+2,-1)
2->R	( 0, 0)	(-2, 0)	(+1, 0)	(-2,+1)	(+1,-1)
2->L	( 0, 0)	(+2, 0)	(-1, 0)	(+2,+1)	(-1,-1)
L->2	( 0, 0)	(+1, 0)	(-2, 0)	(+1,+2)	(-2,-1)
L->0	( 0, 0)	(-2, 0)	(+1, 0)	(-2,+1)	(+1,-2)
0->L	( 0, 0)	(+2, 0)	(-1, 0)	(-1,+2)	(+2,-1)

Arika 认为，当 I 转向水平朝向、或从水平朝向旋转时，其踢墙应关于 y 轴对称，故做出如此修改。下面的例子给出了这一更改的一大影响：

若从阴影位置右转，基准和 Arika 的 SRS 都可完成消四。

若镜像，只有 Arika SRS 可通过左转成消四。

Arika SRS 也允许这样的旋转（右转）。然而基准 SRS 中，无论是左转还是右转都会旋入左侧无法消四。

值得注意的是，这样的更改使得 I 块的踢墙不再具有基准版工作原理中所述的性质（或不能再用此种方式分析）。

评价

SRS 虽在多人对战中有良好的表现，但在高重力模式下更易出现失误，因此经常受到玩家的诟病。
与此同时，一些经典方块玩家指责 SRS 的移动重置过分降低了游戏的难度^{[需要来源]}。

优点

• 原位旋转符合物理直觉，新手玩家也能快速掌握。

	SRS: 零重力下 严谨一致的旋转			ARS: 朝上的姿态 略显奇怪			MTC: 旋转中心 位于方块外部			Atari: 方块靠左上角 对齐

• SRS 的踢墙允许方块进入原本无法到达的位置。

• 踢墙也衍生出了多种多样的 T 旋构造。

绯红之王

T3 塔

Trinity

DT 炮

TD 攻击

皇家十字

• 四种朝向的 S、Z、I 允许玩家做到更高效的极简操作。

	逆时针旋转 类似向左移动一格。 逆转+左移≈左移两格。			顺时针旋转 类似向右移动一格。 顺转+右移≈右移两格。

• 几乎每种旋转都可逆。即每种踢墙都有其相反方向的对应。

4w 中决定是否打出 Mini T1

缺点

• SRS 中，方块以朝上的姿态生成，加上没有 (0,1) 这种原地上踢，贴地旋转会导致偏移。
  • ARS、DTET 等旋转系统由于方块朝上时位置偏下一格，无此问题。

• 对于 SZ 两块，这样的踢墙极其迷惑，顺时针的踢墙类似没有踢墙的逆时针旋转，反之亦然。

		S 块落地前 进行顺时针旋转				S 块落地前 进行逆时针旋转
		S 块落地后 进行顺时针旋转				S 块落地后 进行逆时针旋转

• 低重力下，部分踢墙会导致方块永远不会触及地面，导致无限拖延。
  • 多数较新的方块游戏（如 TGM3、Techmino 等）采取有限重置/踢墙次数，限制了这种无限拖延的操作。

• 位移了两格及以上的踢墙不太符合常理，可能需要特别记忆。

旋转中心下移两格， 被命名为大外回旋

T3

• 下图中，Z 块无法顺时针旋转，所有踢墙尝试全部失败（S 块在镜像地形中亦然）。这种情况在 20G 环境下尤其突出。

• 一些本符合直觉的踢墙，SRS 反而不会检测（如向下踢墙一格）。

ARS 中可行。

ARS 中可行。

C2 中可行。

C2 中可行。

C2 中可行。

• 四个朝向的 S、Z 块导致踢墙时必须记忆方块朝向。有时必须是逆转两次，而有时必须是顺转两次。

必须是顺转两次。

必须是逆转两次。

• I 块的踢墙不对称。这意味着有些情况下 I 块可以踢入，而镜像的场地中却无法踢入。这一点饱受玩家诟病。
  • 一些官方（如 TGM3）或非官方游戏（如 TETR.IO、Techmino）自创的旋转系统对 I 块的踢墙表做了微调，令其更加合理。

左转可进入。

镜像地形却无法踢入。

• 若堆叠极高，或处于 20G 状态，常常很难将 I 块竖直丢入右列。仍是由于踢墙表的不对称，从初始姿态，I 块会朝错误的方向踢墙，方块需要旋转三次才能到达想要的位置。

		当从朝上的姿态旋转时 方块先向左踢墙。				当从朝下的姿态旋转时 方块先向右踢墙。

外链

• Jagorochi 关于 SRS 踢墙的分析（存档）